Lezione 19 - Le funzioni

La funzione valore assoluto

La funzione $f\left( x \right)=\left| x \right|$ è nota come funzione valore assoluto o modulo.

Per ogni valore di x, la funzione valore assoluto è uguale a x per x positivo, a –x per x negativo e a 0 per x = 0.

Facciamo alcuni esempi:

per x = 3 si ha $f\left( 3 \right)=\left| 3 \right|=3$
per x = 5 si ha $f\left( 5 \right)=\left| 5 \right|=5$
per x = –3 si ha $f\left( -3 \right)=\left| -3 \right|=3$
per x = –5 si ha $f\left( -5 \right)=\left| -5 \right|=5$
per x = 0 si ha $f\left( 0 \right)=\left| 0 \right|=0$

In generale la funzione valore assoluto può essere scritta anche in questo modo:

\[ f\left( x \right)=\left| x \right|=\left\{ \begin{array}{l} x & \mathrm{se }& x\ge 0 \\ -x & \mathrm{se }& x\lt 0 \\ \end{array} \right. \]

Il grafico della funzione valore assoluto$~f\left( x \right)=\left| x \right|$ è quindi:

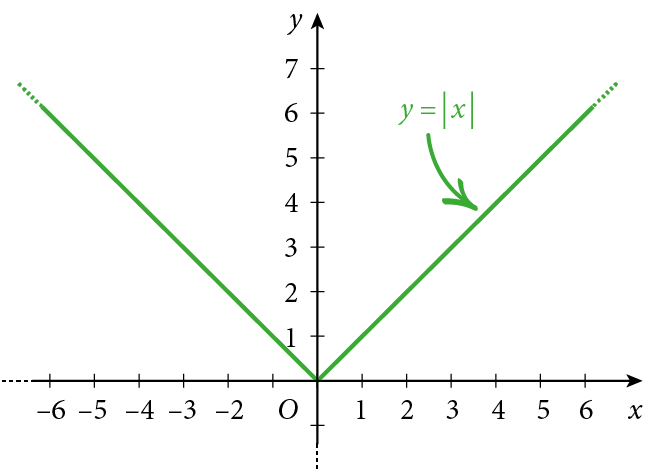
Di seguito alcune caratteristiche della funzione valore assoluto:

passa per l’origine degli assi
passa per tutti i punti di coordinate (k;k) e (–k;k), con k numero reale
è una funzione pari
è decrescente per x < 0 e crescente per x > 0
il suo dominio è $\left] -\infty ;+\infty \right[$
assume un valore minimo per x = 0, coincidente con l’origine
il suo codominio è $\left[ 0;+\infty \right[$

Ora possiamo studiare le caratteristiche di grafici di altre funzioni in cui è presente il valore assoluto.

La funzione $f\left( x \right)=\left| x+1 \right|$

Scriviamo la funzione in questa forma:

\[ f\left( x \right)=\left| x+1 \right|=\left\{ \begin{array}{l} x+1 & \mathrm{se } & x+1 \ge 0 \\ -x-1 & \mathrm{se } & x+1 \lt 0 \\ \end{array}= \right. \\ \left\{ \begin{array}{l} x+1 & \mathrm{se } & x \ge -1 \\ -x-1 & \mathrm{se } & x\lt -1 \\ \end{array} \right.\]

e disegniamo il suo grafico:

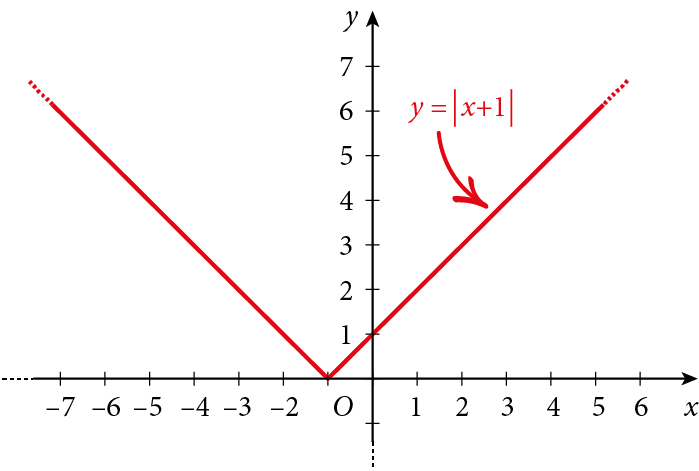
Puoi notare che la funzione $f\left( x \right)=\left| x+1 \right|$ si ottiene dalla funzione $f\left( x \right)=\left| x \right|$, effettuando una traslazione di 1 verso sinistra.

La funzione $f\left( x \right)=\left| x \right|+1$

Scriviamo la funzione in questa forma:

\[f\left( x \right)=\left| x \right|+1=\left\{ \begin{array}{l} x+1 & \mathrm{se } & x\ge 0 \\ -x+1 & \mathrm{se } & x \le 0 \\ \end{array} \right.\]

e disegniamo il suo grafico:

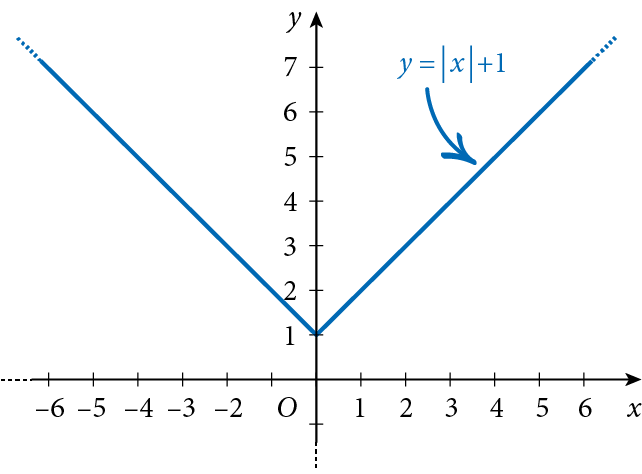
Puoi notare che la funzione $f\left( x \right)=\left| x \right|+1$ si ottiene dalla funzione $f\left( x \right)=\left| x \right|$, effettuando una traslazione di 1 verso l’alto.

La funzione $f\left( x \right)=\left| x+2 \right|-1$

Scriviamo la funzione in questa forma:

\[f\left( x \right)=\left| x+2 \right|-1=\left\{ \begin{array}{l} x+2-1 & \mathrm{se } & x+2\ge 0 \\ -x-2-1 & \mathrm{se } & x+2\lt 0 \\ \end{array}= \right.\\ \left\{ \begin{array}{l} x+1 & \mathrm{se } & x\ge -2 \\ -x-3 & \mathrm{se } & x\lt -2 \\ \end{array} \right.\]

e disegniamo il suo grafico:

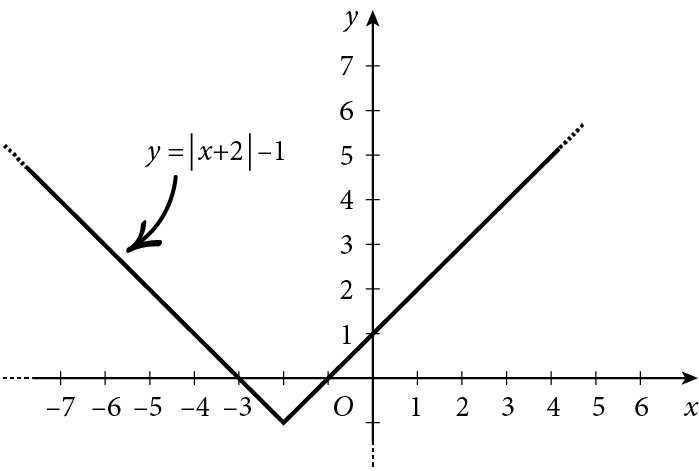
Puoi notare che la funzione $f\left( x \right)=\left| x+2 \right|-1$ si ottiene dalla funzione $f\left( x \right)=\left| x \right|$, effettuando una traslazione di 2 verso sinistra e una traslazione di 1 verso il basso.

La funzione $f\left( x \right)=\left| {{x}^{2}}-1 \right|$

Disegniamo il grafico della funzione $f\left( x \right)={{x}^{2}}-1$

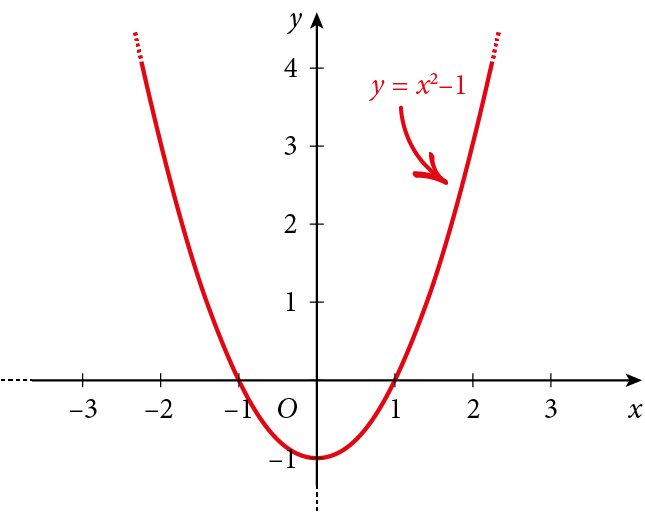
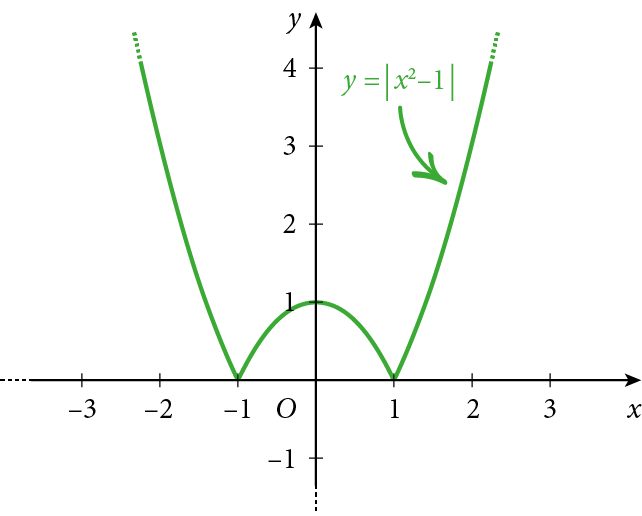
Il grafico della funzione $f\left( x \right)=\left| {{x}^{2}}-1 \right|$ si ottiene lasciando invariate le parti di grafico della funzione $f\left( x \right)={{x}^{2}}-1$ al di sopra dell’asse delle x o coincidenti con esso ed effettuando una simmetria rispetto all’asse delle ascisse per le parti di grafico al di sotto dell’asse delle x, come mostrato in figura: