Lezione 19 - Le funzioni
Le funzioni potenza
Le funzioni potenza sono del tipo $f(x) = x^N$ con $N$ che assume un valore naturale, diverso da 0.
- Per $N$ = 1 la funzione potenza diventa una retta: $y = x$. La retta $y = x$ è la bisettrice del primo e del terzo quadrante.
- Per $N$ = 2 la funzione potenza diventa una parabola con vertice nell’origine e concavità rivolta verso l’alto: $y = x^2$.
Per capire le proprietà delle funzioni potenza è utile disegnarne i grafici distinguendo due casi:
- esponente $N$ pari
- esponente $N$ dispari
Le funzioni potenza con esponente $N$ pari

Le funzioni potenza con $N$ pari sono simmetriche rispetto all’asse delle ordinate, ossia sono funzioni pari.
Di seguito alcune caratteristiche delle funzioni potenza con $N$ pari:
- passano per l’origine degli assi
- passano per i punti $(1;1)$ e $(-1;1)$
- sono funzioni pari
- sono decrescenti per $x \lt 0$ e crescenti per $x \gt 0$
- il loro dominio è $\left]-\infty;+\infty\right[$
- assumono un minimo per $x = 0$, coincidente con l’origine e il loro codominio è $\left[0;+\infty\right[$
Le funzioni potenza con esponente $N$ dispari
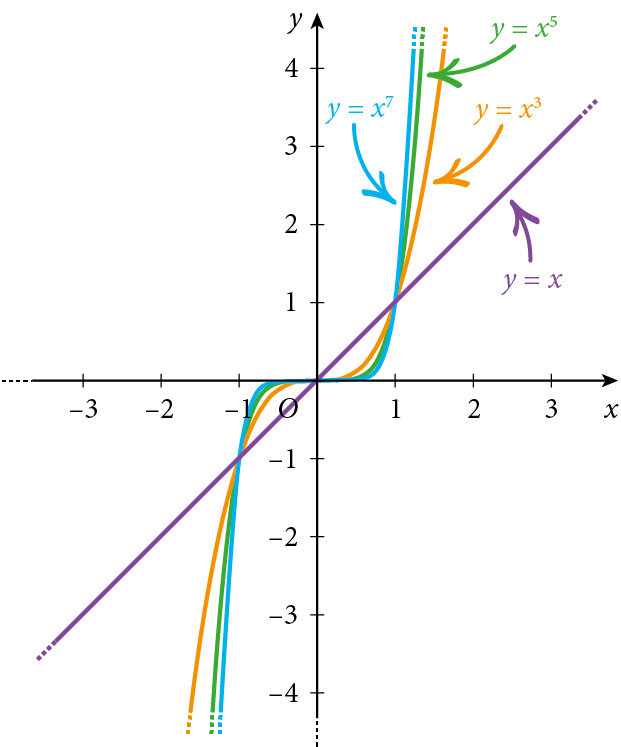
Le funzioni potenza con $N$ dispari sono simmetriche rispetto all’origine degli assi, ossia sono funzioni dispari.
Di seguito alcune caratteristiche delle funzioni potenza con $N$ dispari:
- passano per l’origine degli assi
- passano per i punti $(1;1)$ e $(-1;-1)$
- sono funzioni dispari
- sono crescenti per ogni valore di $x$
- il loro dominio è $\left]-\infty;+\infty\right[$
- il loro codominio è $\left]-\infty;+\infty\right[$
Copyright © 2023 Zanichelli editore S.p.A.
