Lezione 19 - Le funzioni

Funzioni del tipo $f(x) = 1/(ax+b)$ con $a$ e $b$ costanti assegnate

Le funzioni del tipo $f\left( x \right)=\frac{1}{ax+b}$ sono particolari iperboli equilatere.

Una iperbole è equilatera se i suoi asintoti sono perpendicolari.

Le funzioni $f\left( x \right)=\frac{1}{ax+b}$ hanno un asintoto orizzontale e un asintoto verticale.

L’asintoto orizzontale coincide con l’asse delle ascisse e ha quindi equazione $y = 0$.

L’asintoto verticale è parallelo all’asse delle ordinate e ha equazione $x = –b/a$.

La funzione $f\left( x \right)=\frac{1}{ax+b}$ passa per il punto $(0;1/b)$.

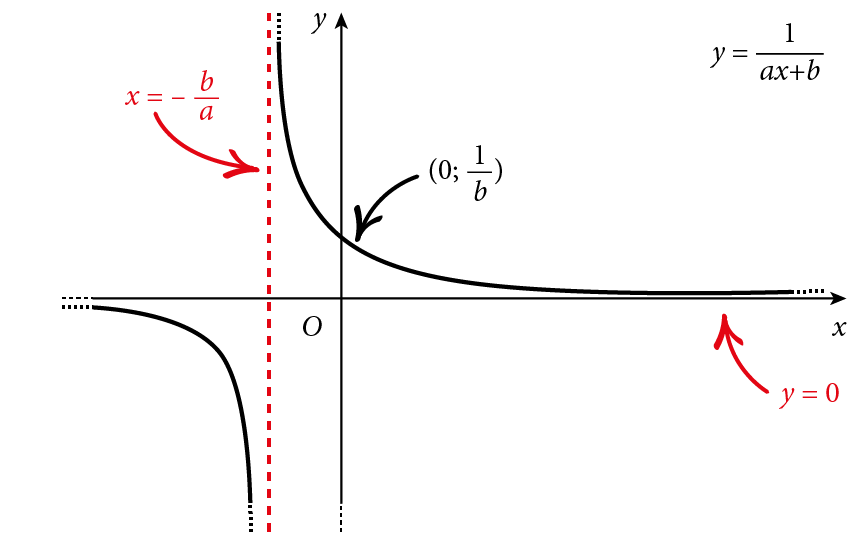
I due asintoti dividono il piano in 4 parti:

se $a \gt 0$, i due rami di iperbole si trovano nel quadrante in alto a destra e in basso a sinistra; in ogni ramo, l’iperbole decresce;
se $a \lt 0$, i due rami di iperbole si trovano nel quadrante in alto a sinistra e in basso a destra; in ogni ramo, l’iperbole cresce.

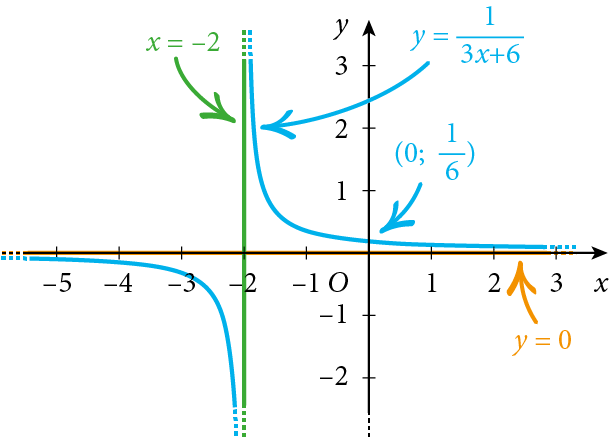
Esaminiamo per esempio la funzione $f\left(x\right)=\frac{1}{3x+6}$, con $a = 3$ e $b = 6$:

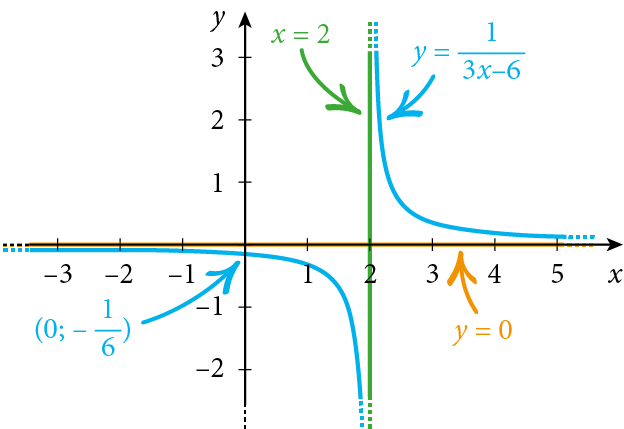
Esaminiamo per esempio la funzione $f\left(x\right)=\frac{1}{3x-6}$, con $a = 3$ e $b = -6$:

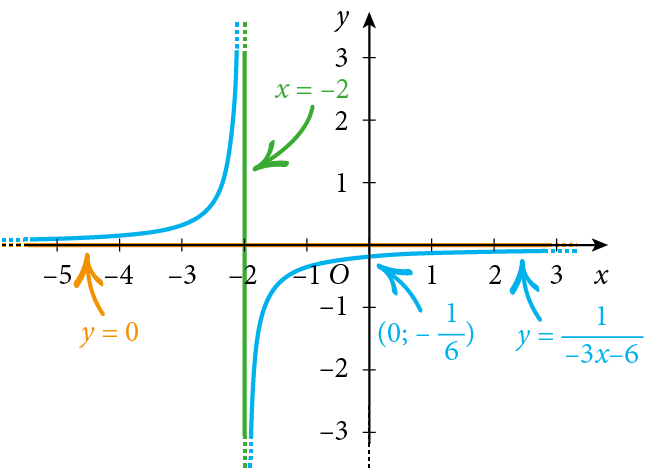
Esaminiamo per esempio la funzione $f\left(x\right)=\frac{1}{-3x-6}$, con $a = -3$ e $b = -6$:

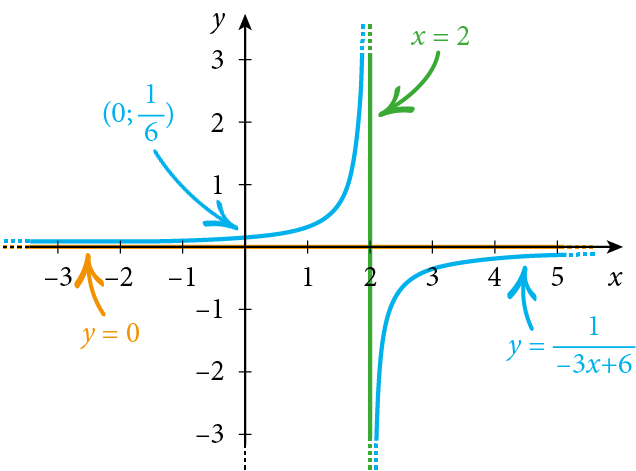
Esaminiamo per esempio la funzione $f\left(x\right)=\frac{1}{-3x+6}$, con $a = -3$ e $b = 6$: