Lezione 19 - Le funzioni

Equazioni e disequazioni del tipo $f(x) = g(x), f(x)>a$

È interessante usare un metodo grafico per poter risolvere alcune equazioni o disequazioni.

A titolo di esempio, riportiamo alcuni esercizi risolti.

Esempio svolto

Quante soluzioni esistono per l’equazione $\sin x=5/7$?

Soluzione

Disegniamo le funzioni $y=\sin x$ e $y=5/7$ e determiniamo con un metodo grafico il numero di soluzioni:

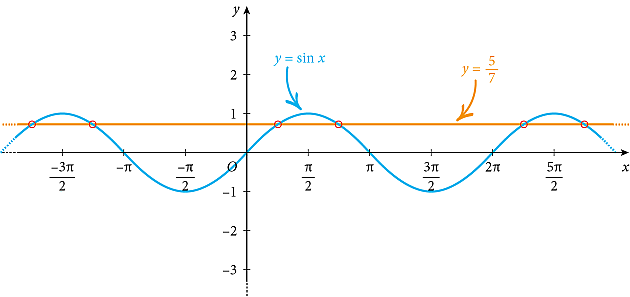
Dai grafici puoi notare che esistono infiniti punti di intersezione delle due funzioni.

L’equazione $\sin x=5/7$ ha infinite soluzioni. Le soluzioni $x$ dell’equazione sono espresse dalle ascisse dei punti di intersezione delle due funzioni.

Esempio svolto

Quante soluzioni esistono per l’equazione $2^x=-x+3$?

Soluzione

Disegniamo le funzioni $y=2^x$ e $y =-x+3$ e determiniamo con un metodo grafico il numero di soluzioni:

Dai grafici puoi notare che esiste un unico punto di intersezione delle due funzioni.

L’equazione $2^x=-x+3$ ha una e una sola soluzione. In particolare, le due funzioni hanno intersezione per $x = 1$. La soluzione dell’equazione è quindi $x = 1$.

Esempio svolto

Quante soluzioni esistono per l’equazione $2^{-x}=-x^2 + 2$? Riesci a stimare il valore numerico delle soluzioni?

Soluzione

Disegniamo le funzioni $y=2^{-x}$ e $y =-x^2+2$ e determiniamo con un metodo grafico il numero di soluzioni:

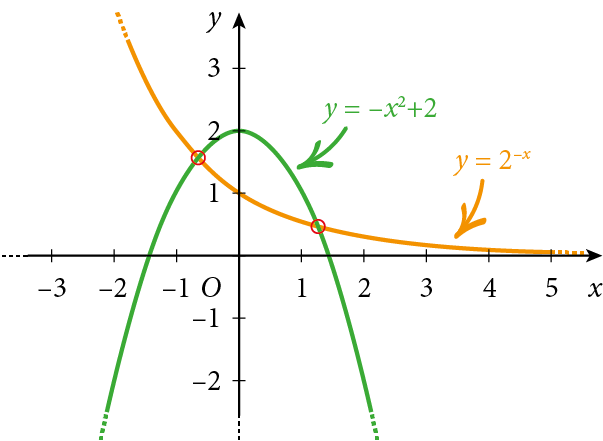
Dai grafici puoi notare che esistono due punti di intersezione delle due funzioni.

L’equazione $2^{-x}={-x}^2+2$ ha due soluzioni. In particolare, le due funzioni hanno intersezione in un punto di ascissa compreso tra $–1$ e $0$ e in un altro punto di ascissa compreso tra $1$ e $2$. Le soluzioni dell’equazione sono quindi due e possiamo anche stimare il loro valore.

Una soluzione è compresa tra $–1$ e $0$; l’altra soluzione è compresa tra $1$ e $2$.

Esempio svolto

Risolvi con il metodo grafico la disequazione $3^x \gt 2$.

Soluzione

Disegniamo le funzioni $y=3^{x}$ e $y = 2$ e determiniamo con un metodo grafico per quali valori delle ascisse la funzione $y=3^x$ risulta maggiore di $2$:

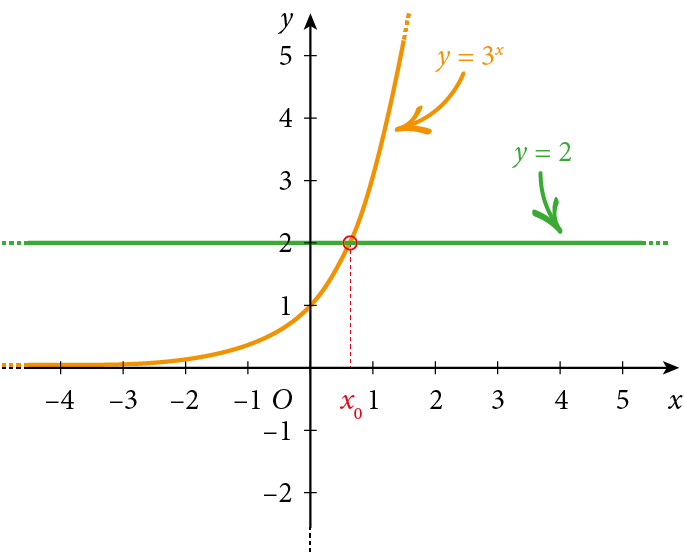
Dai grafici puoi notare che la funzione $y=3^x$ risulta maggiore di $2$ per $x \gt x_0$, con $0 \lt x_0 \lt 1$.

La disequazione $3^x\gt 2$ è quindi soddisfatta per $x \gt x_0$, con $0 \lt x_0 \lt 1$.