Lezione 23 - La probabilità

I diagrammi ad albero

Nella teoria delle probabilità è molto utile considerare uno schema grafico, detto diagramma ad albero.

Esempio svolto

Qual è la probabilità che lanciando un dado si ottenga il 5 e lanciando una moneta si ottenga testa?

$\frac{1}{24}$
$\frac{1}{8}$
$\frac{5}{8}$
$\frac{1}{12}$
$\frac{1}{16}$

Soluzione

Si hanno i seguenti eventi:

$E_1$ = «esca 5 con il lancio del dado»
$E_2$ = «esca testa con il lancio della moneta»

Primo metodo (probabilità del prodotto logico di eventi)

Dato che i due eventi sono indipendenti, si ha:

\[\text{P}(E_1 \cap E_2) = \text{P}(E_1)\text{P}(E_2) = \frac{1}{6}\cdot\frac{1}{2} = \frac{1}{12}.\]

Secondo metodo (il diagramma ad albero)

Disegniamo il diagramma ad albero dei due eventi, considerando prima il lancio del dado e poi il lancio della moneta.

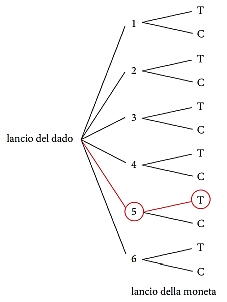
Il numero totale dei rami è $12$ (eventi possibili), mentre è solo uno il ramo, in rosso, relativo all’evento favorevole («esca 5 con il lancio del dado» e «esca testa con il lancio della moneta»).

La probabilità richiesta è quindi:

\[P(E_1 \cap E_2) = \frac{\text{eventi favorevoli}}{\text{eventi possibili}} = \frac{1}{12}\]

La risposta corretta è la D.