Lezione 23 - La probabilità

La probabilità condizionata

Eventi dipendenti ed eventi indipendenti

Consideriamo una scatola contenente 9 palline: 3 rosse, 2 blu e 4 gialle.

Estraiamo una pallina per due volte consecutive. La seconda pallina viene estratta dopo aver rimesso la prima nella scatola.

Consideriamo gli eventi

$E_1$ = «la prima pallina estratta è rossa»,
$E_2$ = «la seconda pallina estratta è gialla».

Gli eventi $E_1$ ed $E_2$ sono indipendenti, perché la seconda estrazione non è influenzata dalla prima.

Se invece la prima pallina estratta non viene rimessa nella scatola, gli eventi $E_1$ ed $E_2$ sono dipendenti, perché il verificarsi o il non verificarsi di $E_1$ cambia il numero dei casi favorevoli per $E_2$.

Due eventi $E_1$ ed $E_2$ sono:

indipendenti se il verificarsi di uno non influenza la probabilità di verificarsi dell’altro;
dipendenti in caso contrario.

In generale, diamo la seguente definizione.

Dati due eventi $E_1$ ed $E_2$, con $p(E_1) \neq 0$, si chiama probabilità condizionata di $E_2$ rispetto a $E_1$ la probabilità che si verifichi $E_2$ nell’ipotesi che $E_1$ sia verificato, e si indica con $p(E_2|E_1)$.

Se $p(E_2|E_1) = p(E_2)$, cioè le conoscenze ulteriori sul verificarsi di $E_1$ non modificano la probabilità di $E_2$, gli eventi sono indipendenti.

Se invece $p(E_2|E_1) \neq p(E_2)$, cioè le conoscenze ulteriori sul verificarsi di $E_1$ modificano la probabilità di $E_2$, gli eventi sono dipendenti.

Calcolo della probabilità condizionale

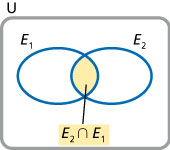
Chiamiamo $k$ il numero degli esiti favorevoli al verificarsi di $E_1$ e $r$ quello degli esiti favorevoli al verificarsi di $E_2$ nell’ipotesi che $E_1$ si sia verificato, ossia il numero di elementi di $E_2 \cap E_1$. Per definizione, abbiamo:

\[p(E_2|E_1)=\frac{r}{k}\]

Dividiamo numeratore e denominatore per $n$, numero degli elementi di $U$:

\[p(E_2|E_1)=\frac{r}{k}=\frac{\frac{r}{n}}{\frac{r}{n}}=\frac{p(E_2\cap E_1)}{p(E_1)}\]

Per la probabilità condizionata vale quindi il seguente teorema.

Teorema

La probabilità condizionata di un evento $E_2$ rispetto a un evento $E_1$, non impossibile, è:

$p\left(E_2 \mid E_1\right)=\frac{p\left(E_2 \cap E_1\right)}{p\left(E_1\right)}$, con $p(E_1) \neq 0$.

Analogamente:

$p\left(E_1 \mid E_2\right)=\frac{p\left(E_1 \cap E_2\right)}{p\left(E_2\right)}$, con $p(E_2) \neq 0$.

Esempio svolto

In un istituto ci sono 650 alunni, di cui 425 femmine e 225 maschi. Nella classe 5^a B ci sono 24 alunni, di cui 11 femmine e 13 maschi. Si estraggono a sorte due alunni che partecipino a un sondaggio nazionale.

Calcolare la probabilità che gli alunni estratti siano entrambi maschi, sapendo che sono stati estratti due alunni della 5^a B.

Soluzione

Chiamiamo:

$E_1$ = «sono stati estratti due alunni della 5^a B»;
$E_2$ = «sono stati estratti due maschi».

Calcoliamo $p(E_2|E_1)$ applicando il teorema della probabilità condizionata.

$E_2\cap E_1$ = «sono stati estratti due maschi della 5^a B».

Casi favorevoli:

$C_{13,2}=\frac{13\cdot 12}{2}=78$

Casi possibili:

$C_{650,2}=\frac{650\cdot 649}{2!}=210\,925$

Quindi:

$p(E_2 \cap E_1) = \frac{C_{13,2}}{C_{650,2}}=\frac{78}{210\,925}=\frac{6}{16\,225}$.

La probabilità di estrarre due alunni della 5^a B è:

$p\left(E_1\right)=\frac{C_{24,2}}{C_{650,2}}=\frac{\frac{24 \cdot 23}{2}}{210925}=\frac{276}{210925}$.

La probabilità di estrarre due alunni maschi, sapendo che sono stati estratti due alunni della 5^a B è:

$p\left(E_2 \mid E_1\right)=\frac{p\left(E_2 \cap E_1\right)}{p\left(E_1\right)}=\frac{6}{16225} \cdot \frac{210925}{276}=\frac{13}{46}$.